Tabung adalah salah satu bentuk bangun ruang yang memiliki peran penting dalam matematika dan berbagai bidang ilmu lainnya. Dalam artikel ini, kita akan menjelajahi definisi dan sifat tabung, serta rumus-rumus yang digunakan untuk menghitung luas permukaan dan volume tabung, lengkap dengan contoh soal untuk memperjelas konsepnya.

 

1. Definisi & Sifat Tabung

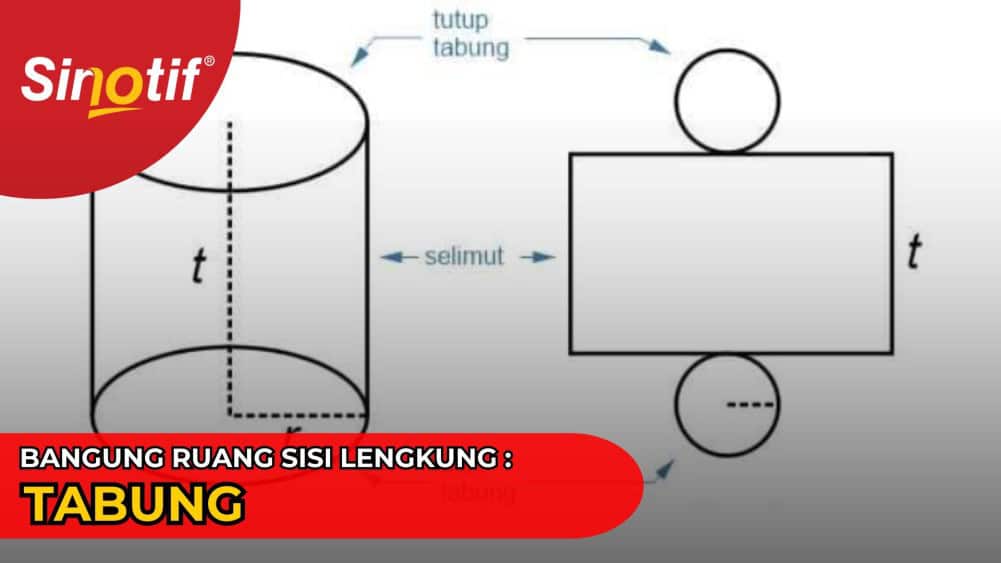
Tabung adalah bangun ruang yang terbentuk oleh dua lingkaran sejajar yang sama ukuran dan sebuah permukaan tabung (selimut tabung) yang berbentuk persegi panjang yang menghubungkan kedua lingkaran tersebut. Sifat-sifat tabung meliputi :

• Mempunyai 2 rusuk

• Alas dan tutup berbentuk lingkaran

• Mempunyai 3 bidang sisi (alas, selimut, tutup)

Sumber : www.pelajaran.co.id

 

2. Rumus Luas Permukaan Tabung

Luas permukaan tabung dapat dihitung dengan menjumlahkan luas ketiga sisinya, yaitu

Luas Permukaan Tabung = Luas Alas + Luas Atap + Luas Selimut Tabung

Luas alas = luas atap = π r²

Luas selimut tabung  = 2 π r t

Luas Permukaan Tabung = π r² + π r² +2 π r t = 2 π r²+2 π r t = 2 π r (r+t)

Jadi, 

L = 2 π r (r+t)

Keterangan :

L = Luas permukaan tabung

π = 22/7 atau 3,14

r = jari – jari alas / atap

t = tinggi tabung

 

Contoh Soal 1

Sebuah tabung memiliki jari-jari lingkaran alas sebesar 5 cm dan tinggi 10 cm. Hitunglah luas permukaan tabung tersebut.

 

Pembahasan 

Diketahui ???? = 5 cm, t = 10 cm .

Maka Luas permukaan tabung tersebut

L = 2 π r (r+t) = 2 π 5 (5+10) = 10 π(15) = 150π≅417,24 cm²

 

Jadi, luas permukaan tabung tersebut adalah sekitar 471,24 cm².

 

3. Rumus Volume Tabung

Volume tabung dapat dihitung dengan mengalikan luas alas tabung dengan tingginya

V = Luas alas x tinggi

V = nr² x t

Jadi, volume tabung adalah

V=πr² t

 

Di mana:

???? adalah volume tabung.

???? adalah jari-jari lingkaran alas atau tutup.

? adalah tinggi tabung.

 

Contoh Soal 2

Sebuah tabung memiliki jari-jari lingkaran alas sebesar 3 cm dan tinggi 8 cm. Hitunglah volume tabung tersebut.

Pembahasan 

Diketahui: ???? = 3 cm, t = 8 cm. 

Maka 

V = πr² t

V = π(3)² 8

V = 72 n ≅ 226,20 cm²

Jadi, volume tabung tersebut adalah sekitar 226,20 cm³.

 

Rumus-rumus luas permukaan dan volume tabung memungkinkan kita untuk menghitung berbagai ukuran dan parameter yang berkaitan dengan bentuk ini. Dengan pemahaman yang kuat tentang konsep tabung dan rumus-rumusnya, kita dapat mengaplikasikannya dalam berbagai situasi, baik dalam matematika maupun dunia nyata.

~Suci